Kontakt
Prof. Dr.-Ing. habil. Sven Grundmann
Statikgebäude (Haus IV) / Raum 105
Albert-Einstein-Straße 2
18059 Rostock
Fon +49 (0) 381 498 - 9310
Fax +49 (0) 381 498 - 9312
sven.grundmannuni-rostockde
Übersicht
Kompaktkurs(e)
Kompaktkurs(e) Strömungsmechanik
im Sommersemester 2021
MRT kompakt: Magnetresonanz, Bildgebung und Strömungsvisualisierung
Kristine John, M.Sc., Dr.-Ing. Martin Bruschewski
Universität Rostock, Lehrstuhl Strömungsmechanik
Veranstaltungsinformationen
| Kompaktkurs | Blockveranstaltung 0,5 SWS |
|---|---|
| Termin und Ort | Vorlesung, Praktikum Projektwoche im Sommersemester 2021 (eintägig) |
| Zielgruppe | Studierende der Masterstudiengänge, wissenschaftliche Mitarbeiterinnen und Mitarbeiter. |
Inhalt des Kompaktkurses
In diesem Kompaktkurs sollen die Grundlagen der Magnetresonanztomographie (MRT) und deren Anwendungs-möglichkeiten im Ingenieurswesen vermittelt werden.
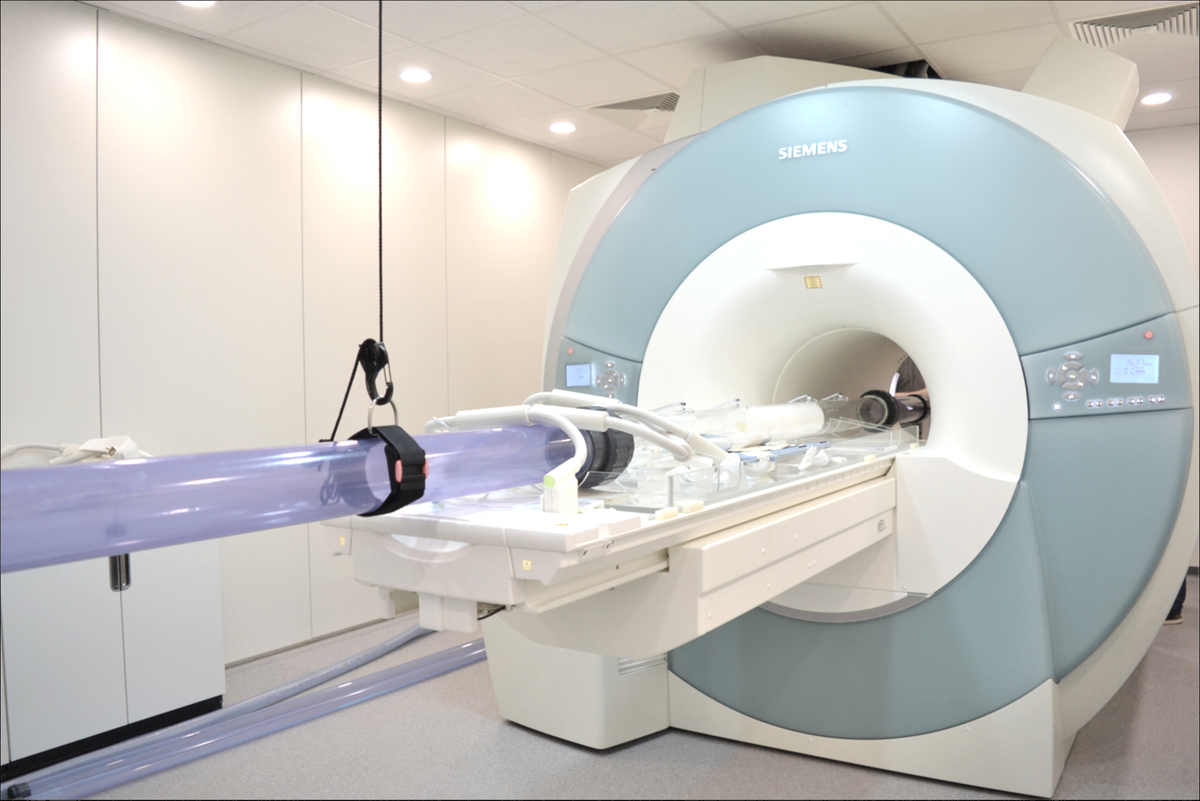
Die MRT ist ein aus der Medizin bekanntes Bildgebungsverfahren, welches auch für die Erfassung von 3D Geschwindigkeitsdaten in Strömungen eingesetzt werden kann. Zwar kann zum jetzigen Zeitpunkt noch nicht die gleiche Auflösung wie in den üblichen Messverfahren erreicht werden, allerdings können mit der MRT vergleichsweise schnell und kostengünstig experimentelle Daten erzeugt werden.
Während die MRT in der Medizin seit Jahrzehnten routiniert angewendet wird, ist ihr Einsatz in den Ingenieurswissenschaften derzeit noch stark eingeschränkt. Dies liegt vor allem daran, dass die MRT nicht wie eine klassische Messtechnik verwendet werden kann. In vielen Bereichen wird die MRT die üblichen Messverfahren nicht ablösen können. Vielmehr ergeben sich mit der MRT komplett neue Anwendungen, die zuvor aufgrund der fehlenden Messtechnik nicht untersucht werden konnten.
Als Ziel dieses Kurses sollten Sie nach erfolgreicher Teilnahme in der Lage sein, die Grundlagen der MRT und die Rahmenbedingungen bei der Durchführung von MRT-Messungen zu verstehen. Zusätzlich werden Sie argumentieren können, welche Problemstellungen aus den Ingenieurswissenschaften besonders geeignet bzw. ungeeignet für eine MRT-Untersuchung sind.
Mustererkennung in der Strömungsmechanik – Strategien und Anwendungsbeispiele
Dr.-Ing. Jochen Kriegseis
Karlsruhe Institute of Technology, Institute of Fluid Mechanics
Veranstaltungsinformationen
| Kompaktkurs | Blockveranstaltung 1,0 SWS |
|---|---|
| Termin und Ort | Vorlesung, Übung/Praktikum Projektwoche im Sommersemester 2021 (zweitägig) |
| Zielgruppe | Studierende der Masterstudiengänge, wissenschaftliche Mitarbeiterinnen und Mitarbeiter. |
Inhalt des Kompaktkurses
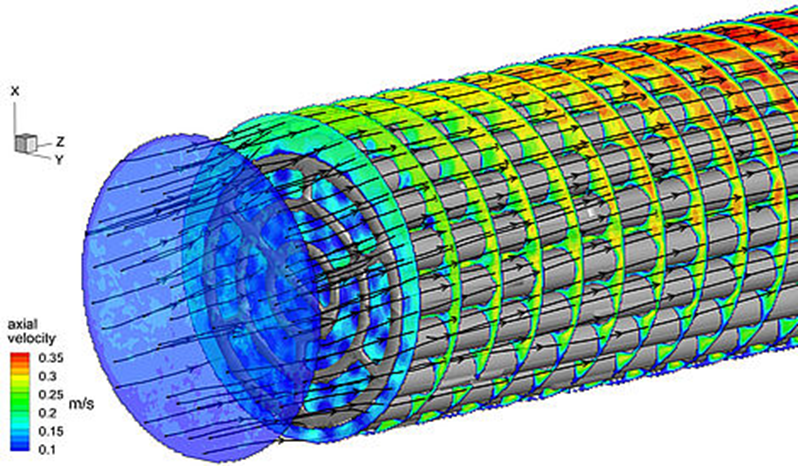
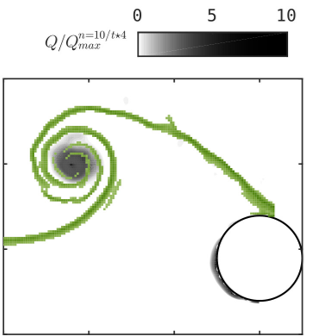
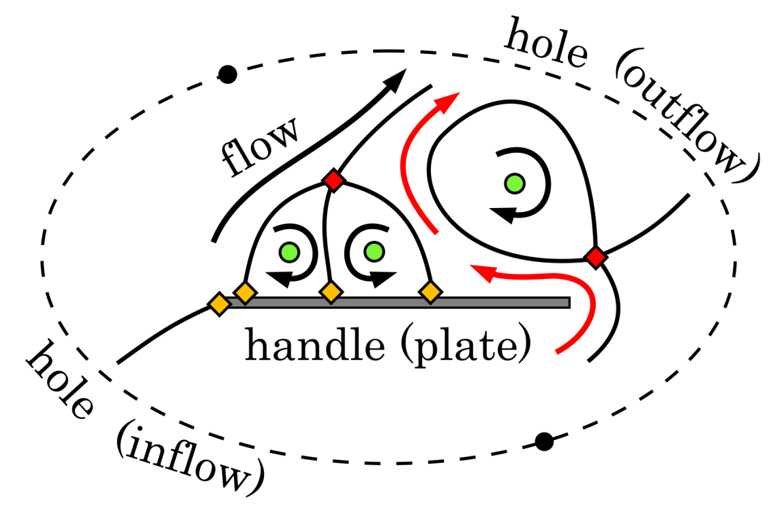
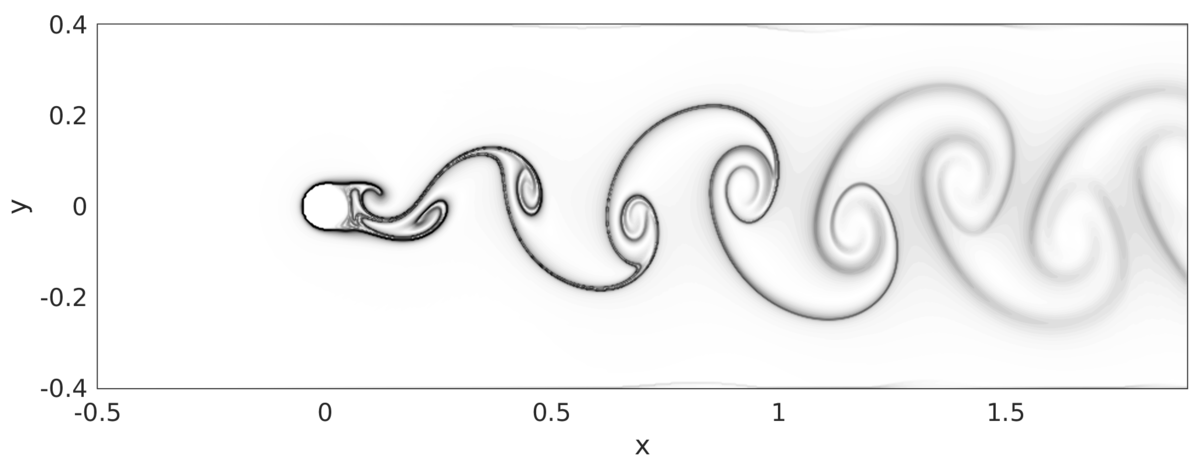
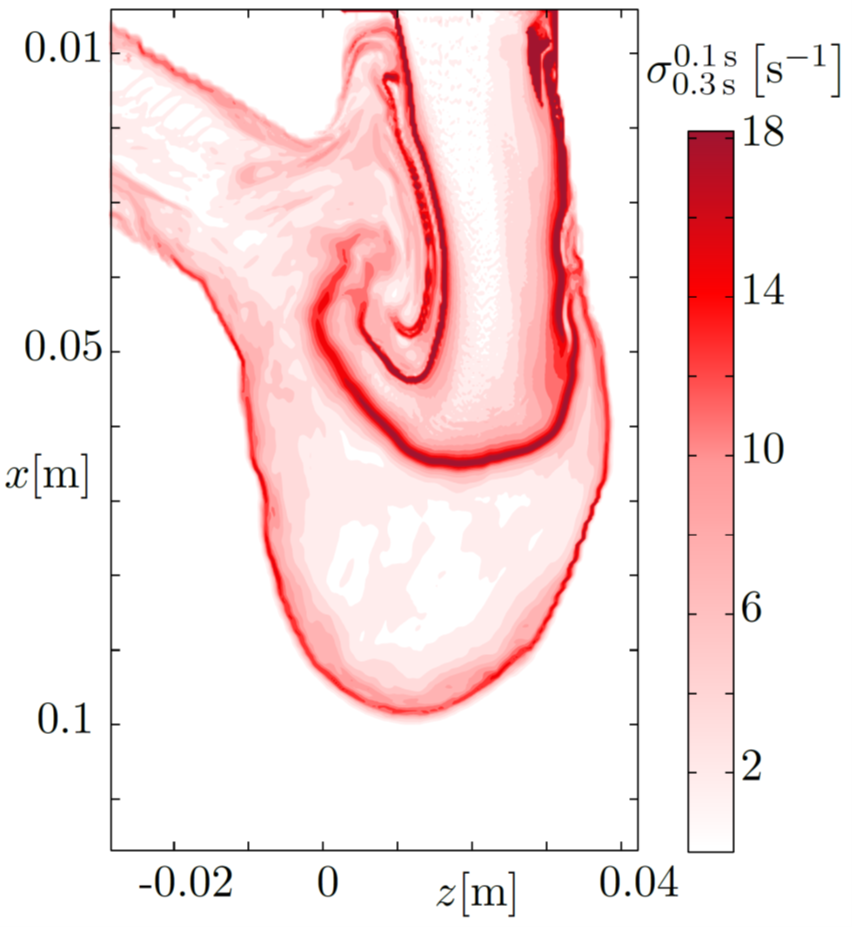
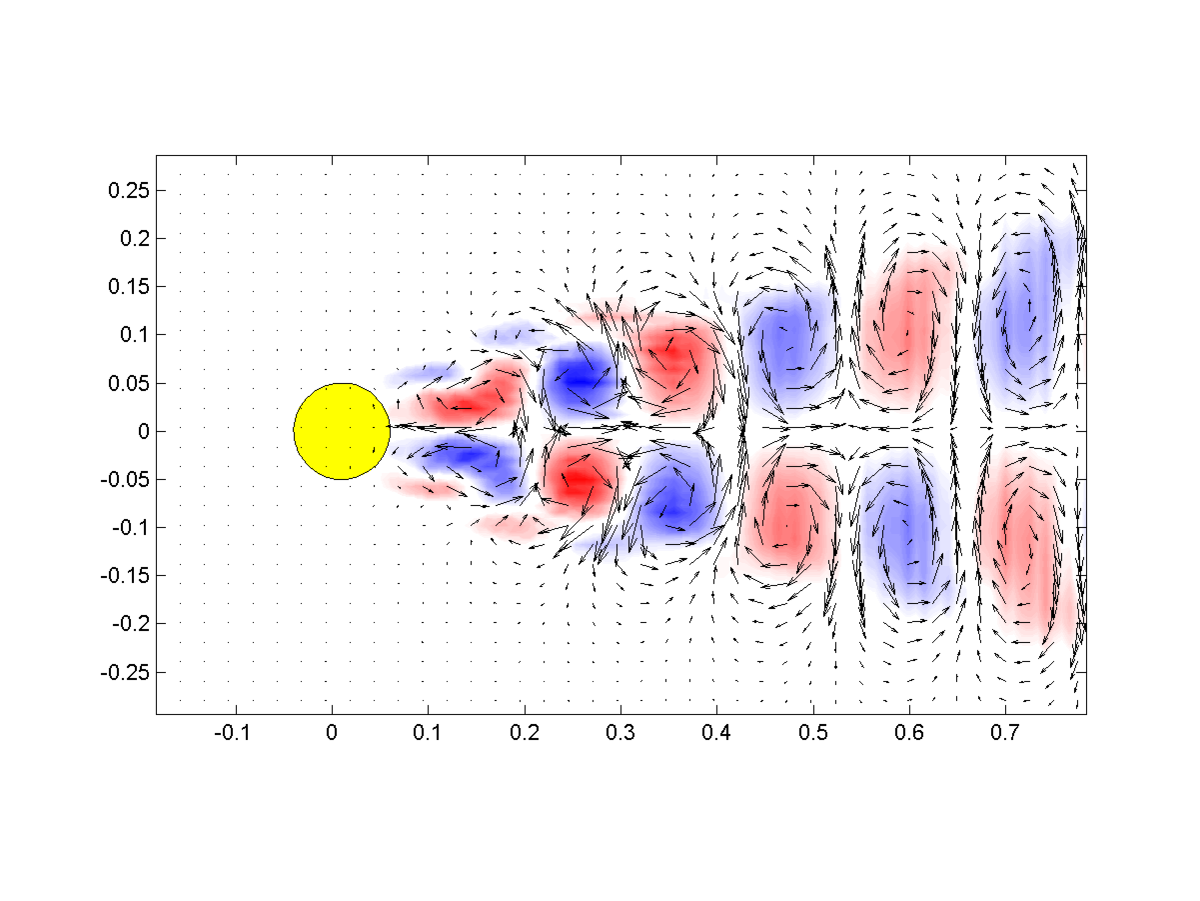
Entstehung, Dynamik und Lebensdauer strömungsmechanischer Strukturen dominieren eine Vielzahl verschiedenartiger Strömungssituationen in der Natur und bei technischen Anwendungen. Eine zuverlässige Identifikation derartiger Strömungsmuster und Interpretation der extrahierten Strukturen ist daher sowohl im Bereich der Grundlagenforschung als auch bei anwendungsnahen Optimierungsansätzen von großer Bedeutung. Während sich die ersten dokumentierten Bemühungen des 15. Jahrhunderts noch mit der Anfertigung und Beschreibung von Skizzen begnügen mussten, existiert heute eine Vielzahl verschiedener (computergestützter) Analysestrategien mit unterschiedlichen Schwerpunkten und Komplexitätsstufen.
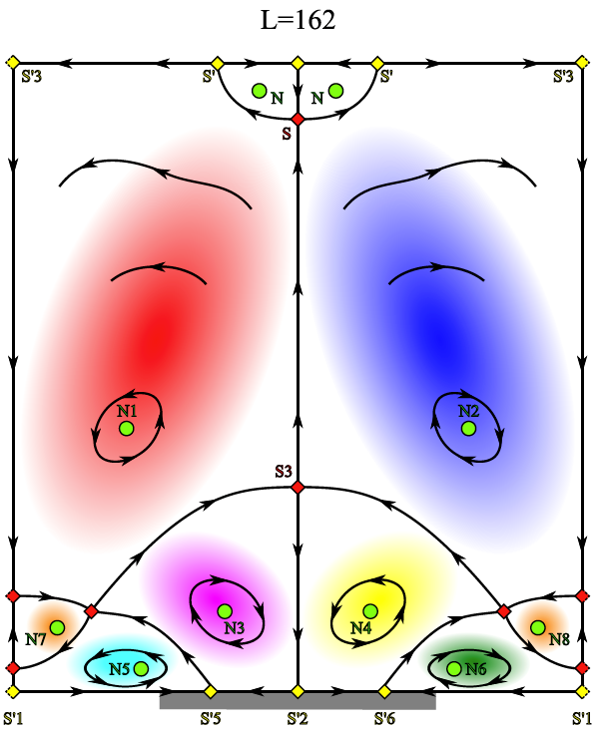
In diesem Kompaktkurs soll ein Einblick in die große Bandbreite der möglichen Analysetechniken gegeben werden, wobei eine Auswahl verschiedener Identifikationstechniken vorgestellt wird. Ein wichtiger Aspekt bei der Auswahl ist die grundlegende Unterscheidung zwischen rein topologischen, (lokalen) Euler'schen, Lagrange'schen und modalen Ansätze. Im ersten Teil des Kurses werden die folgenden Methoden daher zunächst entsprechend klassifiziert und danach im Detail behandelt:
- Topologie-/Singularitätenanalyse,
- Q-Kriterium,
- Delta-Kriterium,
- Lambda-2-Kriterium,
- Swirl Strength,
- Finite-Time Lyapunov Exponent / Lagrangian Coherent Structures (FTLE/LCS),
- Residence Time,
- Particle Tracking,
- Reynolds Decomposition,
- Triple Decomposition,
- Proper Orthogonal Decomposition (POD, CPOD),
- Singular Value Decomposition (SVD),
- Dynamic Mode Decomposition (DMD).
Im zweiten Teil des Kurses werden einige der Methoden in Matlab implementiert und an Beispieldaten getestet, sodass die konkrete Umsetzung der verschiedenen Ansätze zur Vertiefung des Erlernten beitragen kann. Als Ziel dieses Kurses sollten Sie nach erfolgreicher Teilnahme in der Lage sein, die grundlegenden Strategien der behandelten Methoden zu erläutern und gegeneinander abzugrenzen. Zusätzlich können Sie argumentieren, welche Methoden besonders (un)geeignet für welche Art Strömungsprobleme sind.